Razlika med konkavnimi in konveksnimi mnogokotniki

priljubljenih primerjav

Ključna razlika: mnogokotnik, katerega notranji koti so manjši od 180 stopinj, je znan kot konveksni poligon. Po drugi strani pa se poligon z enim ali več notranjimi koti, ki je večji od 180 stopinj, imenuje konkavni mnogokotnik.

Poligon lahko definiramo kot zaprto ravninsko figuro (dvodimenzionalno obliko), ki je sestavljena iz treh ali več segmentov črte. Poligone lahko razdelimo na več vrst. Ena taka vrsta temelji na notranjih kotih. Konveksni poligon je tisti, v katerem nobeden od kotov ne kaže navznoter. Z drugimi besedami, nima notranjega kota, ki je večji od 180 stopinj.

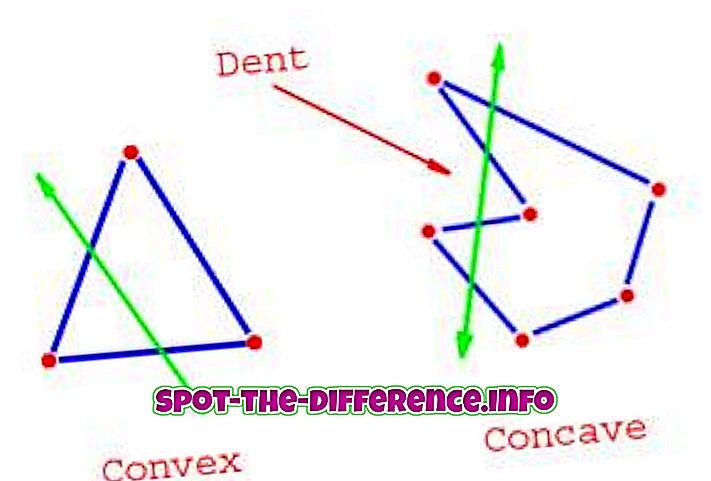
Poligon s katerim koli notranjim kotom, ki je večji od 180 stopinj, je znan kot konkavni mnogokotnik. Z drugimi besedami, konkavni mnogokotnik obstaja z notranjim refleksnim kotom. Preprost test lahko uporabimo za razlikovanje konkavnega poligona s konveksnim poligonom. Če je narisana črta, ki gre skozi mnogokotnik, in vedno gre skozi samo dve od linij ali poligonov, ki sestavljajo obliko, je v tem primeru oblika poligona konveksna. Po drugi strani pa, če se isti postopek ponovi v konkavni obliki, potem lahko črta prečka več kot dve vrsti. V tridimenzionalnih oblikah se lahko izvede isti preskus, da se razlikuje med obema.

Pomembno je omeniti, da so vse diagonale konveksnega poligona povsem znotraj poligona. Vendar pa bodo v konkavnem poligonu nekatere diagonale vedno ležale zunaj poligona. Vsi pravilni mnogokotniki so konveksni (poligon, ki ima vse strani enake in so vsi notranji koti enaki). Konveksne poligone je lažje narisati v primerjavi z konkavnimi poligoni.

Primerjava med izbočenimi in konkavnimi mnogokotniki:

	Konkavni mnogokotnik	Konveksni mnogokotnik
Opredelitev	Poligon z enim ali več notranjimi koti, ki je večji od 180 stopinj, se imenuje konkavni mnogokotnik.	Poligon, katerega notranji koti so manjši od 180 stopinj, je znan kot konveksni poligon.
Lastnosti	Vsaj en notranji kot je večji od 180 stopinj Lahko se razreže v niz izbočenih ravnin. Poligon, ki ni konveksni poligon, imenujemo konkavni mnogokotnik.	Vsak notranji kot je manjši od 180 stopinj. Vsak odsek med dvema tockama poligona ne gre zunaj poligona (tj. Ostane znotraj ali na meji poligona). Vsaka navpična ali vodoravna os seka največ dvakrat.
Prepoznavanje funkcije	Zob (krivulja navznoter)	Vse njene črte so zunaj
Razlikovalna značilnost	Linija vsebuje stran mnogokotnika, ki vsebuje točko na notranjosti poligona.	Nobena vrstica, ki vsebuje stran mnogokotnika, ne vsebuje točke v notranjosti poligona.
Načine za ustvarjanje	Veliko	Primerjalno malo
Cross izdelek	Navzkrižni produkt sosednjih vektorskih parov je <0	Navzkrižni produkt sosednjih robov bo istega znaka (to je z-komponenta)
Primer	Oris črke "W"	Trikotnik

Razlika med LG Optimus L5 II, L5 II Dual in Xolo Q800

Ključna razlika: LG Optimus L5 II in njegov nasprotni del LG Optimus L5 II Dual sta dva pametna telefona, ki sta v začetni stopnji. LG Optimus L5 II in L5 II Dual sta si zelo podobna, vendar se razlikujeta v nekaterih krajih, vključno z videzom. Naprava je opremljena s 4-palčnim True IPS LCD kapacitivnim zaslonom na dotik, ki ponuja gostoto približno 233 ppi. Xol