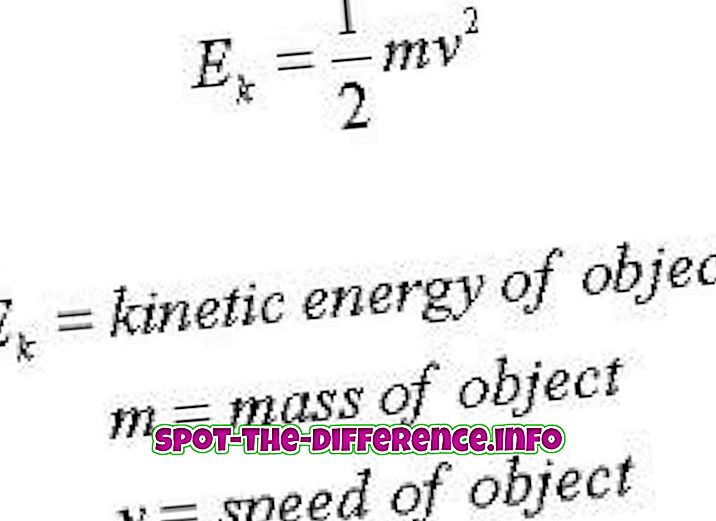Ključna razlika: Parabola je stožčasti odsek, ki nastane, ko ravnina reže konično površino vzporedno s stožcem. Hiperbola nastane, ko ravnina reže konično površino vzporedno z osjo.

Parabola in hiperbola sta dve različni besedi, odseki in enačbe, ki se v matematiki uporabljajo za opis dveh različnih delov stožca. Te se razlikujejo po obliki, velikosti in drugih dejavnikih, vključno s formulami, ki se uporabljajo za izračun. Da bi jih razumeli, najprej razumemo stožec in različne konične dele.

Stožčasti odsek je krivulja, ki se dobi, ko se ravnina križa s stožcem na različne načine. Odrezki, ki jih dobimo iz presečišča, vključujejo elipso, krog, parabolo in hiperbolo. V skladu z analitično geometrijo je konika definirana kot "ravninska algebraična krivulja stopnje 2". Priljubljena definicija stožnice vključuje točko fokusa, linijo directrix in ekscentričnost. Pričakuje se, da bo točka izostritve in direktne linije v fiksnem obroku v stožnici. Razmerje je znano kot ekscentričnost stožnice. Ekscentričnost elipse, parabole in hiperbole se razlikujejo; elipse imajo ekscentričnost manjšo od 1, parabole imajo ekscentričnost, ki je enaka 1, hiperbole pa imajo ekscentričnost večjo od 1. Najstarejša znana dela na stožnicah segajo v četrto stoletje pred našim štetjem. rešiti problem podvojitve kocke z uporabo parabole.

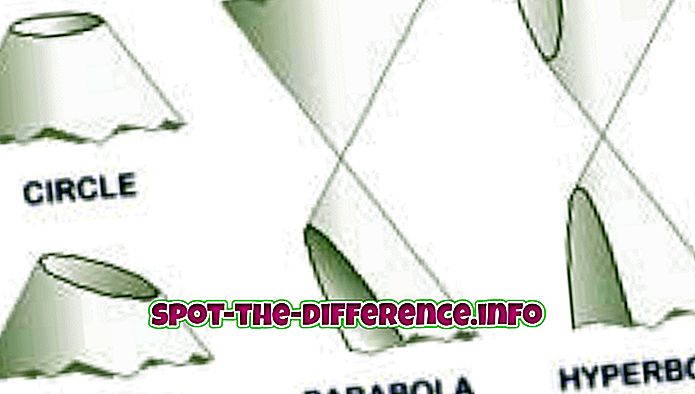
Parabola je konični del, ki se ustvari, ko se ravnina križa s stožcem. Parabolae ali parabole tvorijo "od sečišča desne krožne stožčaste površine in ravnine, ki je vzporedna z ustvarjanjem ravne črte te površine." Še en način, kako nastane parabola, je, ko lokus točk na ravnini, ki je enako oddaljena od žarišča, in directrix ustvari parabolo. V algebri se parabole pogosto uporabljajo v grafih kvadratnih funkcij z uporabo formule y = x ^ 2.

Linija, ki razdeli parabolo skozi sredino, je znana kot os simetrije; ta linija je prav tako pravokotna na directrix in poteka skozi žarišče. Točke, ki so na osi simetrije, ki sekajo parabola, se imenujejo "vertex". Razdalja med vrhom in žariščem je znana kot "goriščna razdalja". Parabole se lahko odprejo v obe smeri, vključno gor, dol, desno ali levo. Tudi glavna značilnost parabol je, da so vsi enaki, le različni po velikosti. Lahko se premaknejo in natančno prilagodijo, da ustrezajo katerikoli drugi paraboli. Parabole se uporabljajo v različnih aplikacijah, kot so avtomobilski reflektorji, oblikovanje balističnih izstrelkov itd. Prav tako imajo pomembno vlogo v fiziki, inženirstvu, matematiki itd.

Hiperbole so gladka krivulja, ki se pojavi, ko se ravnina križa s stožcem, ki je vzporeden z osjo y, kar ustvarja rez ob strani stožca. Hiperbola je opredeljena z njenimi geometrijskimi lastnostmi ali enačbami, za katere je postavljena rešitev. Izraz "hiperbola" izhaja iz grške besede, ki pomeni "preveč vržene" ali "pretirane". Ta izraz je skoval Apolonij iz Perge, ki je veliko prispeval k študiju stožnic.

Znano je, da ima hiperbola veje, ki so zrcalne slike med seboj in podobne dvema neskončnima lokoma. Točke na obeh vejah, ki so najbližje drug drugemu, se imenujejo tocke. Vrstica, ki povezuje vozlišča, je znana kot prečna os ali glavna os, ki ustreza velikemu premeru elipse. Središče prečne osi je znano kot središče hiperbole. Enačba hiperbole je zapisana kot x2 / a2- y2 / b2 = 1. Hiperbolo uporabljamo v različnih aplikacijah v današnjem svetu, vključno s potjo, ki ji sledi senca konice sončne ure, oblika odprte orbite; uporablja se kot lok v mnogih zgradbah, kot enačbe iz matematike in geometrije, fizike itd.

Hiperbole in parabole sta odprti krivulji, kar pomeni, da se ne končata in se neomejeno nadaljujeta do neskončnosti, kar elipse in krogi ne morejo storiti.